Hohmann transfer orbit from Earth to Mars

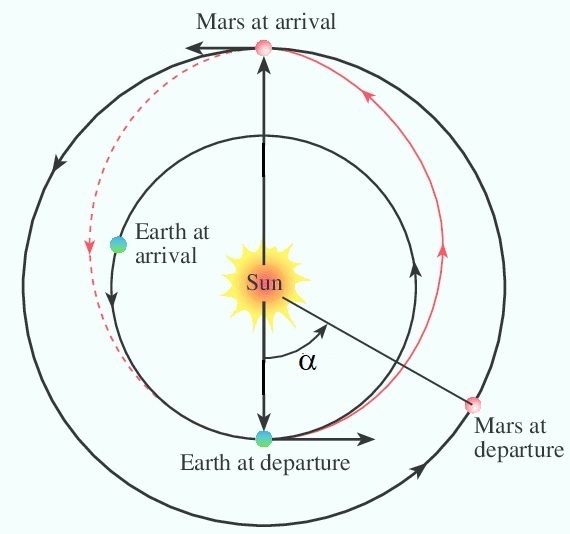
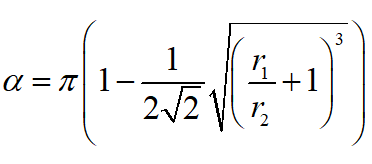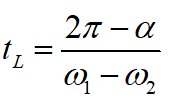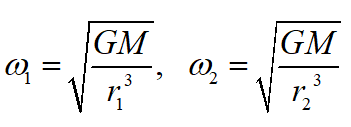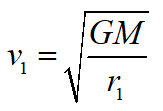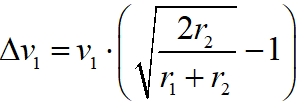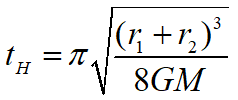A Hohmann orbit is the trajectory of a spacecraft between two nearly circular orbits requiring the least fuel. In this simulation we will study a Hohmann orbit of a space probe between the orbits of Earth and Mars. It is an ellipse with the perihelion (the point closest to the sun) at the orbit of Earth, and the aphelion (the point farthest from the sun) at the orbit of Mars.
To achieve the correct ellipse the velocity of the spacecraft must be increased by the correct amount at the correct time. At the correct time the angle Earth-Sun-Mars must have a value given by a formula in the right column. See the figure below. This angle is zero when the simulation starts.

In the right column you will find formulas to calculate the Hohmann orbit.
The assumptions made to derive these formulas are:

1) The orbits of the planets are circular and in the same plane
2) The space probe starts so far from Earth that the gravitational influence of Earth on the space probe can be neglected
3) The velocity increase of the space probe is instantaneous
4) The gravitational attraction of Mars on the space probe when it approaches Mars is neglected.

In practice one must allow for all of these factors, and the time of launch, velocity increase and the exact orbit must be calculated numerically.

To simplify, Earth is not included in the simulation, but the space probe initially follows Earth's orbit. The orbits of Earth and Mars are assumed to be perfect circles.

Exercise

1. Calculate the time of launch, the necessary velocity increase and the transit time of the Hohmann orbit.
2. Start the simulation and let it run until the simulated time equals the calculated time of launch (approximately one revolution of Mars). Slow down the simulation when this time approaches so you can stop it as accurately as possible.
3. Choose the menu Miscellaneous, Change Velocities. Click to show the velocity of the space probe with respect to the sun or the center of mass. Add the necessary velocity increase of the space probe to obtain a new value of the velocity and enter it in the v field. When you click Update velocity you can see that the vx- and vy-components are increased in the same proportion so that the direction of the new velocity is still tangential to the orbit of the Earth. Click Exit.
4. Start the simulation again and hope for the best! Slow down the simulation when the space probe approaches Mars. Watch the distance Space probe - Mars and stop the simulation when the space probe is approximately 20 000 km from Mars; otherwise it will collide with Mars.
   If your space probe didn't arrive at Mars, you may find the correct values here.
5. Check if the transit time of the space probe in the simulation fits the calculated time.
6. Choose Miscellaneous, Change Velocities. Show the velocity of the space probe with respect to Mars. Your task: Change the velocity components to bring the space probe into a circular orbit about Mars with radius equal to your stop distance in e. Try out your calculations by restarting the simulation. If necessary, zoom in or out in the second viewport.